Journal of University of Chinese Academy of Sciences

Numerical simulation of surface deformation in Sichuan-Yunnan region considering the drag forces underneath the lower crust

YIN Di, DONG Peiyu, SHI Yaolin

2021, 38 (1): 1-8. DOI: 10.7523/j.issn.2095-6134.2021.01.001

Abstract ( 446 ) PDF (0KB) ( 0 )

In the Sichuan-Yunnan region, GPS observations reveal that the direction of movement is east-southeast, showing a clockwise rotation trend. In previous studies, it is noted that the lower crust of this region is ductile and moves faster than the brittle upper crust. Consequently, there is a drag force on the bottom of the upper crust, which is the main factor causing the distinct movement characteristics. Therefore, in the study of numerical simulation of regional deformation, it is not enough to consider only the elastic factor, but also the drag force. The distribution of the regional drag force is usually calculated by manual partitioning and trial and error method, which relies on subjective judgment. In this study, a two-dimensional elastic plane model is established based on the regional tectonic activities and the GPS observations as the constrained condition. The regional drag force inversion calculated through the polynomial fitting relationship between the residual values (ΔUx, ΔUy) and the coordinates of each observation point. And the residual values are the difference between the simulation result without the drag force and the observation data. The result shows that the drag force is mainly concentrated in the rhombus block, and the value in the north part is the largest (1e8 N), which is in the south direction. The drag force in the south of the block is gradually decreasing (4e7 N), and the direction is gradually diverted to the east and west sides. Finally, the drag force is applied to the finite element model in the form of equivalent body force, and the simulated result is in good agreement with the observation data. This method provides a new idea for the study of long-term deformation in Sichuan-Yunnan region, which is more reasonable and simpler.

Mass migration of Qinghai-Tibet Plateau studied by using GRACE time-variable gravity

RAO Weilong, ZHANG Lan, WANG Qiuyu, TANG He, SUN Wenke

2021, 38 (1): 9-22. DOI: 10.7523/j.issn.2095-6134.2021.01.002

Abstract ( 494 ) PDF (0KB) ( 0 )

The complex mass migration in the Qinghai-Tibet Plateau is accompanied by the change of gravity field, and it is an important scientific problem to study the mass migration of the Qinghai-Tibet Plateau by using time-varying gravity. Application of gravity satellite GRACE (gravity recovery and climate experiment) provides an important observation means for us to understand the mass migration characteristics of the Qinghai-Tibet Plateau, and provides a new approach for studying the geodynamics of the Qinghai-Tibet Plateau. Compared with traditional land-based observation, GRACE realizes global and continuous gravity observation, and enable to study the larger scale problems about mass migration, and satellite gravity shows unique advantage in the research over Qinghai-Tibet Plateau areas. This paper reviews the latest progress in the study of mass migration over the Qinghai-Tibet Plateau using time-varying gravity data over the past ten years, especially the research status, scientific achievements, and existing problems of various factors causing mass change (ice and snow melting, lake water level change, groundwater change, tectonic movement, etc.).

The properties of positive solutions for strongly singular equations with singular potential

TANG Lu, SHUANG Zhen, SUN Yijing

2021, 38 (1): 23-28. DOI: 10.7523/j.issn.2095-6134.2021.01.003

Abstract ( 358 ) PDF (0KB) ( 0 )

We discuss the strongly singular equations of matrix-type,

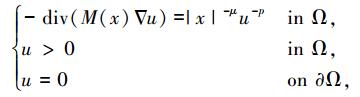
where Ω is a smooth bounded domain in Rⁿ (n ≥ 3) containing the origin, M(x) is a real symmetric matrix on Ω, -3 < -p < -1, and -n < -μ < 0. We show that all H₀¹-solutions are unbounded when -n < -μ < -1-n/2 and there exists no solution of slow growth when M(x)≡I (identity matrix) and -μ<-2.

An iterative construction of Riemann mappings

DENG Fusheng, JIANG Weiwen, ZHANG Xujun

2021, 38 (1): 29-31. DOI: 10.7523/j.issn.2095-6134.2021.01.004

Abstract ( 279 ) PDF (0KB) ( 0 )

In this note, we give an explicit construction of iterative approximation of Riemann mappings. Our method is motivated by Koebe’s proof of the Riemann mapping theorem.

Dynamic TailCoR model and empirical research in financial markets

YE Wuyi, WANG Tainxiong, MIAO Baiqi

2021, 38 (1): 32-40. DOI: 10.7523/j.issn.2095-6134.2021.01.005

Abstract ( 280 ) PDF (0KB) ( 0 )

The research on the correlation between financial markets has been valued by scholars. The occurrence of extreme events such as financial crisis increases the tail correlation between markets. The TailCoR model is a new method for measuring the tail correlation, which decomposes the correlation into linear and nonlinear components and performs well in small samples. In order to describe the dynamic correlation between financial markets, we propose dynamic TailCoR model, and decompose the correlation into dynamic linear and nonlinear correlation coefficients based on the dynamic TailCoR model. The dynamic linear correlation coefficient is estimated based on DCC-GARCH. The remainder of the dynamic TailCoR divided by the dynamic linear correlation coefficient is defined as the dynamic nonlinear correlation coefficient. Finally, based on the dynamic TailCoR model, the tail correlation of the stock returns of the four large domestic banks is studied. It is found that the tail correlations increase significantly in two periods, namely, in 2008 and from 2015 to early 2016, and the tail correlation rise is mainly caused by the nonlinear correlation. The research methods proposed in this paper give dynamic nonlinear correlation metrics, which can be well applied in investment and risk measurement.

The superpotential and geometric invariants of D-brane system on compact Calabi-Yau manifold

LI Fei, YANG Fuzhong

2021, 38 (1): 41-48. DOI: 10.7523/j.issn.2095-6134.2021.01.006

Abstract ( 256 ) PDF (0KB) ( 0 )

The effective D-brane superpotential determines the vacuum structure and is the generating function of the Ooguri-Vafa invariants. It is of great significance in both physics and mathematics. In this work, the superpotential of the system with three D-branes is calculated by mirror symmetry, GKZ-system (hypergeometric system of Gel’fand, Kapranov, and Zelevinski) method, and the type Ⅱ/F-theory duality. On compact Calabi-Yau manifold, the superpotenial and geometric invariants of D-brane system in the three phases are studied. The calculations show that the superpotentials in the three phases are different. This implies that the enhanced gauge symmetry in low energy theory and geometric singularity may lead to the phase transition.

Influence of pulse duration on the supercontinuum generation from femtosecond laser filamentation in fused silica

XU Mengning, ZHAN Lindi, XI Tingting

2021, 38 (1): 49-53. DOI: 10.7523/j.issn.2095-6134.2021.01.007

Abstract ( 325 ) PDF (0KB) ( 0 )

The influences of the pulse duration, chirp， and initial spectrum of the femtosecond laser on the supercontinuum generated in fused silica have been investigated theoretically. Results show that, with the increase of the pulse duration, the cut-off wavelength of the blue-extension becomes longer and the spectral intensity becomes lower at the constant energy. For the laser with pulse duration larger than 150 fs, the spectral intensity of the blue-extension generated by the negatively chirped pulse is higher than those generated by the freely-chirped pulse and the positively chirped pulse.

Electrocapillarity motion of metal droplets

GUO Shengrong, LIU Runcong, DAI Xiaotian, WANG Xiaodong, NA Xianzhao

2021, 38 (1): 54-61. DOI: 10.7523/j.issn.2095-6134.2021.01.008

Abstract ( 341 ) PDF (0KB) ( 0 )

In this paper, the formula of electrocapillary motion was derived theoretically, and the electrocapillary motion of metal droplets in NaOH-starch mixture under the action of gravity was studied by a self-designed experimental apparatus.The electric field was applied in the above simulation system to film the motion track of the metal droplet and conduct image processing to obtain the instantaneous motion rule of the droplet. It is found that after applying electric field, the horizontal velocity component of the droplet goes through three stages:rapidly increasing to a maximum value, slowly decreasing to a stable value, and maintaining a stable velocity.The results show that when the mixture viscosity is between 853-1 760 mPa·s, the electric field intensity is between 90-135 V/m or the droplet radius is between 0.91-1.31 mm, the droplet velocity satisfies the formula of electrocapillary motion, that is, the electrocapillary velocity is proportional to the electric field intensity and droplet radius, and inversely proportional to the mixture viscosity.

Construction of space of information flows and assessment of network resilience from reflexive perspective: a case study of Baidu index in Yangtze River Delta

LI Yan, SUN Yang, CHEN Wen

2021, 38 (1): 62-72. DOI: 10.7523/j.issn.2095-6134.2021.01.009

Abstract ( 323 ) PDF (0KB) ( 0 )

Based on the Baidu index, this paper attempts cross-scale cognition of the physical geographical space and the virtual space of information from individual search actions with integrated methods including network linkage strength, network complexity， and Circos. Further, it interprets the construction of the space of information flows of Yangtze River Delta from a reflexive perspective and evaluates the network resilience of the space of information flows in the region. The main results are as follows: First, the analysis of node hierarchy and density agglomeration demonstrates high network resilience of the space of information flows in the region of Yangtze River Delta, with an overall pattern of “one pole with multiple centers” but with significantly unbalanced density. Second, the analysis of hierarchical transmission and flow matching shows that, on one hand, tourism has higher network hierarchy with the most hierarchical advantages than house prices, weather and talents; on the other hand, Shanghai, Hangzhou, Suzhou, Nanjing, and Ningbo occupy a higher level in the space of information flows of the Yangtze River Delta. Among them, Shanghai, Hangzhou, and Suzhou are the most important nodes for both directions of the information flows in and out. Third, the reflexive perspective exhibits a method for cross-scale geospatial cognition from individual actions to the virtual space of information, and then reflexive to physical geographical space. The network resilience analysis presents that individual actions are territorially reflexive to regional network structure and the resilience of the regional network structure. Moreover, establishing an individual-regional cross-scale spatial linkage through a reflexive perspective contributes to a mutual feedback on the changing individual actions and the regional space, and the analysis of network resilience as an attempt to explore the adaptation to rapidly changing geographical space provides reference for national and regional governance and decision-making.

Analysis of pollution status and main pollution sources of Huaisha River in Beijing

LI Chang, WU Li, HE Yujian

2021, 38 (1): 73-82. DOI: 10.7523/j.issn.2095-6134.2021.01.010

Abstract ( 368 ) PDF (0KB) ( 0 )

Huaisha River is the main source of water in Huairou Reservoir. It is one of the drinking water sources in Beijing. The quality of its water directly affects the health of the citizens in Beijing. The Beijing government requires its quality to meet the second-class water standard. According to the water quality report of Beijing 2017-2018, most of the relevant indicators for the water quality of the Koutou village that is in the downstream area of Huaisha River are relatively good, which meets the requirements of the second type of water. However, the indicators of total phosphorus and total nitrogen often exceed the standard. We tracked the water quality of different sites from Hongjunzhuang village to Tianxianyu village where the water directly flowed into Huairou Reservoir constantly for one year. The survey found that the variation of water quality mainly affected by human activities. The water quality is relatively poor in spring and summer but better during autumn and winter. The main pollutants in the river were total phosphorus and total nitrogen which resulted from substandard domestic sewage discharged by sewage treatment station and phosphorus-containing feed used by fish farms, etc. These factors directly led to water eutrophication of the Huaisha River and caused total phosphorus and nitrogen indexes in downstream water to be inferior to type Ⅳ or even inferior to type Ⅴ, which is far from the requirements of the type Ⅱ water. The current situation poses a serious hidden danger to the safety of drinking water. According to the survey results, this paper proposes some relevant governance programs.

Characteristics of nitrogen and phosphorus release from struvite coated urea and struvite combined with biochar coated urea in calcareous soil

TANG Sichen, YANG Xiaosong, ZHANG Wantong, MU Jing, XIE Zijian, WANG Jinzhi, HU Zhengyi

2021, 38 (1): 83-93. DOI: 10.7523/j.issn.2095-6134.2021.01.011

Abstract ( 418 ) PDF (0KB) ( 0 )

The characteristics of nitrogen (N) and phosphorus (P) release from slow-release urea, developed based on urea (U) as fertilizer core and struvite (S) and biochar (B) as coating materials, are significant for evaluating the application of high N and low P fertilizer in agriculture system. In the present study, the hydrostatic test and soil column intermittent leaching experiment including five treatments (CK, U, S coated urea (USR), S+low proportion of B coated urea (USB1R), S+high proportion of B coated urea (USB2R)) were carried out to investigate the N and P release from individual S coated U and S combined with B coated U in calcareous soil based on analysis of TN, TP, NH₄⁺-N, NO₃^--N, and PO₄^3-. The results showed that release rate of N in slow-release fertilizers based on hydrostatic test was not higher than 15% within 24 h and 80% within 28 d, which meets the standards of the slow-release fertilizer (GB/T 23348—2009). The release rates of N and P in the three slow-release fertilizers swiftly increased in soil for the first 7 days, and then gradually decreased. The release rates of P in the three slow-release fertilizers were in the decreasing order: USB1R (50.9%) > USB2R (38.3%) > USR (10.0%), and the release rates of N were in the order: USB2R (86.2%) > USB1R (83.1%) > USR (74.0%). The release rates of N in slow-release fertilizers were lower by 9-21 percentages than that in urea. The individual S coated urea and S combined with B coated urea showed slow release of N and P in calcareous soil. The actual efficacy of the developed slow-release fertilizers needs to be further verified.

Applicability evaluation of reference crop evapotranspiration models in Turpan

FAN Liufei, YU Yang, TA Zhijie, PI Yuanyue, SUN Lingxiao, YU Ruide

2021, 38 (1): 94-102. DOI: 10.7523/j.issn.2095-6134.2021.01.012

Abstract ( 311 ) PDF (0KB) ( 0 )

Turpan region is a typical dryland area with little rainfall. Annual evaporation is much larger than precipitation. It is one of the most arid regions under severe water scarcity in China. Accurate estimation of reference crop evapotranspiration (ET₀) is the basis for designing farmland irrigation systems and developing the water-saving agriculture in Turpan. Using meteorological data in crop growing season (from April to October) at Turpan observation station from 2000 to 2015, based on linear regression, root mean square error(RMSE), mean absolute error(MAE), and mean relative error(MRE) statistical indices, taking FAO-56 Penman-Monteith(FAO-56 PM) model as the standard, Priestley-Taylor(P-T), Hargreaves-Samani(H-S), Jensen-Haise(J-H), Turc, Makkink-Allen(M-A), Trajkovic(Traj), Makkink-Hansen(M-H), and Berti-Hargreaves(B-H) models were evaluated in Turpan, and the reasons for the model deviations were analyzed. The results are given as follows. 1) All the models showed the unimodal trend during the growing season. H-S, Traj, and B-H models overestimated the monthly ET₀, while other models underestimated the monthly ET₀ in varying degrees. 2) The estimated ET₀ of Traj model was close to that of FAO-56 PM model, with the RMSE, MAE, and MRE values being 6.38 mm, 5.69 mm, and 4.29%, respectively. The simulation accuracy of M-H model was the second, and Turc model had the worst simulation accuracy. 3) R_n and VPD were the main meteorological factors that affected the deviations of the temperature and radiation models. At the same time, the relationship between the ET₀ calculated by the FAO-56 PM model and the pan evaporation was analyzed, which provides a reference for estimating ET₀ in Turpan by using the pan evaporation.

Temperature and precipitation characteristics and spatial stratified heterogeneity in Badain Jaran Desert

NING Wenxiao, LIU Xuyang, WANG Zhenting

2021, 38 (1): 103-113. DOI: 10.7523/j.issn.2095-6134.2021.01.013

Abstract ( 399 ) PDF (0KB) ( 0 )

In this study, the basic characteristics of climate change of Badain Jaran Desert within nearly 60 a is analyzed using linear trend analysis, Mann-Kendall test, cross wavelet, wavelet coherence， and geo-detector methods, based on the temperature and precipitation data from 2016-2018 by an automatic weather station at the center and data from 1960-2018 by 4 weather stations at the margin of the desert. The results show that the annual average temperature of the Badain Jaran Desert increased at a rate of 0.34 ℃/10 a, but increasing trend of annual precipitation was not obvious. Annual precipitation abruptly changed for several times, while annual average temperature showed abrupt change only once in 1990. The mean monthly temperature in the center of the desert was highly similar to that of the marginal areas, while the monthly change trend of precipitation was quite different. The overall relationship between precipitation and temperature was nonlinear at multiple time scales. Precipitation was characterized by spatially stratified heterogeneity, while temperature did not show such character.

Comparison and analysis of three kinds of typical solar system planetary ephemeris

ZHANG Wenzhao, PING Jinsong, LI Wenxiao

2021, 38 (1): 114-120. DOI: 10.7523/j.issn.2095-6134.2021.01.014

Abstract ( 535 ) PDF (0KB) ( 0 )

The US DE series, the French INPOP series， and the Russian EPM series ephemerides are three types of the world’s leading numerical planetary ephemerides. In this paper, the maximum values and the root-mean-squares of the positions of the major planets (including moon) relative to the earth and the barycenter of the solar system in the three numerical ephemerides during one hundred years (1960-2060) are calculated. The results show that the deviation levels of the measurements about the solar system barycenter range from hundred meters to kilometers, and the differences between EPM2017 and the other two are large. Taking the earth as the reference point，the accuracies for Mercury and Venus are at one hundred meter level. The accuracy of Mars ranges from hundred meters to kilometers. The accuracies for Jupiter and Saturn range from several kilometers to tens of kilometers. The accuracies for Uranus and Neptune range from several hundred kilometers to thousands of kilometers. The accuracy of Lunar ephemeris ranges from decimeter to meter, and its radial distance accuracy is at the decimeter level. These results provide support and basis for the cislunar space science experiment and deep space exploration application.

System-level accelerated reliability demonstration testing design based on fuzzy logic and AHP

LI Peng, DANG Wei, LI Tao, Lü Congmin

2021, 38 (1): 121-129. DOI: 10.7523/j.issn.2095-6134.2021.01.015

Abstract ( 290 ) PDF (0KB) ( 0 )

The traditional statistical analysis-based reliability demonstration testing (RDT) requires a large number of samples and long testing time, failing to satisfy the development demand for short cycle and low cost of electronic products nowadays. We propose a system-level reliability accelerated demonstration testing (RADT) program for multi-failure mode products under multiple stresses by combining mathematical statistics and physics of failure (PoF). Based on the principle of allocating reliability target to each environment stress, products are decomposed at four levels, namely function, structure, mechanism, and stress, and the key function, weakness, dominant failure mode, and sensitive stress can be identified, respectively. After level-by-level allocations, the RADT plan and test profile can be established by connecting environmental testing and reliability testing. Firstly, system reliability is apportioned to each environmental stress based on fuzzy logic and analytic hierarchy process. Secondly, the stress-strength interference model is used to deduce the amplification coefficient for each stress. The overall acceleration factor can be derived by the principle of constant acceleration factor, and then the RADT scheme can be designed based on a statistical plan. A case example is presented to illustrate the effectiveness of the proposed approach in comparison with programs of GJB899A and IEC62506.

FACR: a fast and accurate car recognizer

ZHOU Long, WANG Weiqiang, Lü Ke

2021, 38 (1): 130-136. DOI: 10.7523/j.issn.2095-6134.2021.01.016

Abstract ( 527 ) PDF (0KB) ( 0 )

Most existing fine-grained car recognizers have achieved the good performances on various datasets. However, these recognizers usually work inefficiently, and attention regions cannot be accurately localized especially when multiple cars exist. In this work, we propose a fast and accurate car recognizer called FACR, and it has three advantages over the previous approaches as follows. 1) The attention region localization component proposed in this work has high robustness to the background noise in the image. 2) The network structure proposed in this work is relatively simple, and it has higher computational efficiency while maintaining near accuracy. 3) It is the first time to use the hierarchical classification to finely and accurately categorize cars, and to allow a single network to simultaneously recognize car types, manufacturers, car models, and years of manufacture. The experiments are carried out on standard datasets Compcars and Stanford Cars, and the results demonstrate that FACR achieves the competitive performance compared with the-state-of-art methods in terms of both computational efficiency and classification accuracy.

Far-field gain and isolation of orbital angular momentum dual mode multiplexing

CAO Leban, ZHOU Bin, BU Zhiyong, LAN Yun

2021, 38 (1): 137-144. DOI: 10.7523/j.issn.2095-6134.2021.01.017

Abstract ( 453 ) PDF (0KB) ( 0 )

Generating vortex electromagnetic waves carrying OAM (orbital angular momentum) dual-mode multiplexing based on a uniform circular array is studied. Firstly, it theoretically discusses that a uniform circular array can generate OAM vortex electromagnetic waves,three uniform arrays of different structures, excitation settings of array elements and calculation of transmission gain are proposed. Secondly, the influence of the generated OAM dual-mode multiplexed vortex electromagnetic wave on the far-field gain in the main axis direction is discussed from the angles of the array elements in the array, the radius of the array, and the arrangement of the array elements. Finally, the degree of inter-mode interference in OAM dual-mode multiplexing is studied from the arrangement of array elements. The simulation results show that the greater the number of array elements in the circular array,the greater the far-field gain on the main axis; the difference radius in the circular array has a less influence on the far-field gain on the main axis; compared with the single arrangement, the vortex wave generated by the uniform circular array combined by two different arrangement modes has larger far-field gain on the main axis and less inter-mode interference.

Current Issue